
Means of the most recent email address, if any, provided by such party to Varsity Tutors. Infringement Notice, it will make a good faith attempt to contact the party that made such content available by If Varsity Tutors takes action in response to Information described below to the designated agent listed below. Or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one The y values pick back up at the point (2,4) and continue upwards to infinity. Once again, there is a discontinuity in the range, so we again use the union symbol. The green graph picks up at -1.71 and the y values continue upward until they get to 1.256. We use the symbol ("union") to connect the disconnected parts of the graph.

There is a discontinuity between the red and green graphs' y values. We begin at negative infinity and can trace continuously until we get to the point (-5,-5).

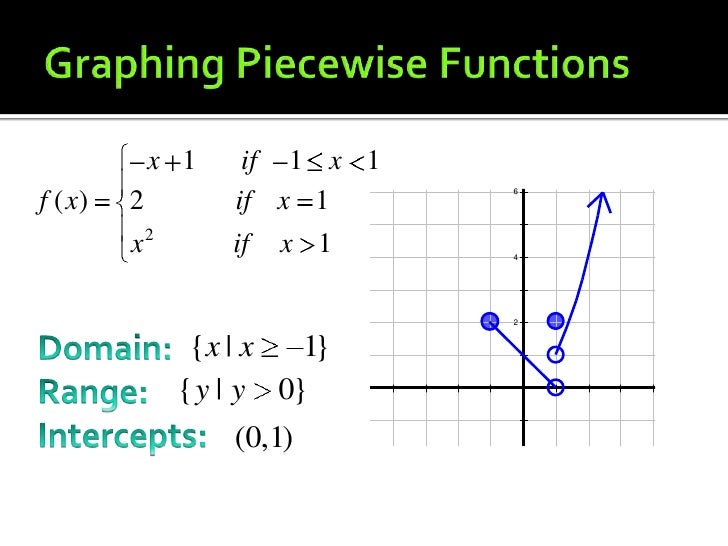
Next, let's start again at the bottom of the graph (in red), this time looking at the y values. Therefore, the domain of this graph is all real numbers or. The purple graph is continuous and goes onwards to positive infinity. Once again, there is no gap in the x values. Then, the graph jumps up to the purple values. You can trace from left to right along the green graph until you get to x=2. While the y values jump, there is no gap in the x values. At this point, it jumps upward to the green graph. You can trace along it continuously until you get to the point (-5,-5). To find the domain, begin at the far left of the graph, starting with the red portion. Because of this, we have to graph them in pieces, too.Firstly, this is a function as it passes the vertical line test. Piecewise functions are defined in terms of pieces of the x-axis there will be difference rules for what x does on each of the various pieces of the graph. (If you would like to study this topic further, please see Graphing Rational Functions.) The above is the kind of graph that your instructor will be looking for. By plotting a few additional points, I was able to nail down specifically what was happening in each region. The horizontal asymptote was just a "suggestion" for the general behavior of the graph when it heads off to either side it means next to nothing in the "middle" near the intercepts, ao I was quite welcome to cross it in near the intercepts. So the asymptotes and intercepts gave me general regions where "stuff" was going on.
That's why I checked points between the x-intercepts and the vertical asymptotes. Note: Occasionally a graph just touches the x-axis at an intercept, instead of going though the axis. On the right, the graph mirrored what happened on the left. In the middle of the graph, between the two vertical asymptotes, there were no x-intercepts, but there were points above the x-axis, so the graph always had to stay above the axis. So, on the left, I knew the graph traced along the horizontal asymptote, came down to cross the axis at x = −3, and then stayed down below the axis, because there was no place (before the vertical asymptote) for the graph to cross the axis to get back above the axis. We can only cross the x-axis at an intercept therefore, if there is no intercept, then there is no crossing of the axis. How did I know which way to go (up or down) at the vertical asymptotes? You can figure this out by looking at the x-intercepts we had.


 0 kommentar(er)
0 kommentar(er)
